Answer:
B.

Explanation:
Since, the amount formula in compound interest,
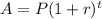
Where, P is the principal amount ( or initial amount ),
r is the annual interest,
t is time ( in years )
Here,
The invested amount is $ 600 at the beginning of year 1,
⇒ P = $ 600
r = 4 % = 0.04
Thus, the amount after n-1 years or the beginning of n years would be,

Which is the required explicit formula,
If n = 5,
Then, the amount at the beginning of 5th year,
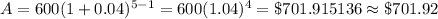
Hence, Option 'B' is correct.