Question

Marquise has 200 meters of fencing to build a rectangular garden. The garden's area (in square meters) as a function of the garden's width w w (in meters) is modeled by: A ( w ) = − w 2 + 1 0 0 w A(w)=−w 2 +100w What side width will produce the maximum garden area? meters

Answer 1

to find the optimized value you need to find where the vertex(tip) of the parabola

use

`- (b)/(2a)`
to find the optimized x value

y= -w^2 +100w + 0


`- (100)/( 2 * - 1)`
x = 50
answer: 50

Answer 2

50 m

Explanation:

We are given that

Width of garden =w

Perimeter of rectangular garden=200 m

We know that

Perimeter of rectangle=
`2(l+ b)`

`200=2(L+w)`

`l+w=(200)/(2)=100`

`L=100-w`

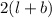
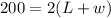
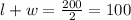
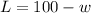
Area of garden
`A(w)=-w^2+100w`

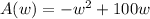
We have to find the side width that will produce the maximum garden area.

Differentiate w.r.t w

`(d(A))/(dw)=-2w+100`

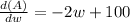
Substitute
`(dA)/(dw)=0`

`-2w+100=0`

`2w=100`

`w=(100)/(2)=50`

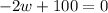
Again differentiate w.r.t w

`(d^2A)/(dw^2)=-2 <0`

Hence, the garden area is maximum at w=50 m

Therefore, width of rectangular garden=50 m