Answer:
Option A- The growth factor of g is twice the growth factor of f.
Explanation:
Given : The equation represents the function f,
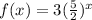
and the graph represents the function g.
To determine : The relationship between the growth factors of f and g.
Solution : First we see that the function g represent in the graph is the exponential growth rate.
So, we can find out the equation of g by looking the points in the graph
The line passing through the points (1,15) and (0,3)
Forming exponential equation from the points.
General form of exponential equation is
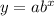
Put point (1,15)
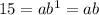 ......[1]
......[1]
Put point (0,3)
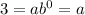 .........[2]
.........[2]
Therefore, a=3 substitute in [1]
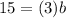
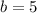
So, The equation of function g is
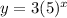
The growth rate of function g is 5
The growth rate of function f is
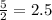
We simply say that the growth factor of g is twice the growth factor of f.
Therefore, Option A is correct.