Question

Write as a product: ac^2–ad+c^3–cd–bc^2+bd

Answer 1

`(a+c-b)(c^(2)-d)`

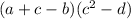
Explanation:

The given equation is:

`ac^(2)-ad+c^(3)-cd-bc^(2)+bd`

We have to simplify it and convert to the product form, therefore taking the common terms from the given expression, we get

`a(c^(2)-d)+c(c^(2)-d)-b(c^(2)-d)`

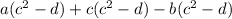
Now, taking
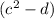`(c^(2)-d)` common from all the terms, we get

`(a+c-b)(c^(2)-d)`

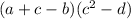
which is the required product form of the given expression.

Answer 2

The product form is
`(c^2-d)(a+c-b)`

Explanation:

Given the expression
`ac^2-ad+c^3-cd-bc^2+bd`

we have to write the above expression as a product.

`ac^2-ad+c^3-cd-bc^2+bd`

Taking a common from first two terms, c from next two and -b from last two terms, we get

`a(c^2-d)+c(c^2-d)-b(c^2-d)`

Now, taking
`c^2-d` common

⇒
`(c^2-d)(a+c-b)`

Hence, the product form is
`(c^2-d)(a+c-b)`