Answer:
Length of diagonal is 18 m
Explanation:
Given in trapezoid ABCD. AC is a diagonal and ∠ABC≅∠ACD. The lengths of the bases BC and AD are 12m and 27m. We have to find the length of AC.
Let the length of diagonal be x m
In ΔABC and ΔACD
∠ABC=∠ACD (∵Given)
∠ACB=∠CAD (∵Alternate angles)
By AA similarity theorem, ΔABC~ΔACD
∴ their corresponding sides are proportional
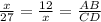
Comparing first two, we get
⇒
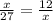
⇒
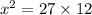
⇒
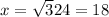
hence, the length of diagonal is 18 m