Answer:
The value of Y is 24 km and distance from A to C to B is AC+Y=18+24=42 km
Explanation:
Given that A highway between points A and B has been closed for repairs. An alternative route between there two locations is to travel between A and C and then from C to B. we have to find the value of Y and the total distance from A to C to B. Let AB=Z
In ΔBCD and ΔABD
∠BCD=∠ABD (∵each 90°)
∠D=∠D (∵common)
By AA similarity, ΔBCD~ΔABD
∴ their corresponding sides are proportional
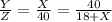
Comparing last two terms, we get

⇒
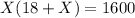
⇒
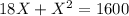
⇒
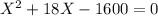
⇒

⇒
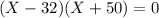
Hence, the roots are X=32, -50
X=-50 not possible as distance can never negative.
Hence, X=32 km
By applying Pythagoras theorem in ΔBCD we get
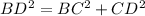

⇒
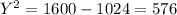
⇒
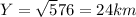
Hence, the value of Y is 24 km and the distance from A to C to B is AC+Y=18+24=42 km