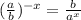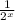Answer:
a.
![-2x\sqrt[3]{x}](https://img.qammunity.org/2023/formulas/mathematics/high-school/jvef05qd9r377gwhjwhlsg6htg9a9yglj9.png)
b.
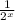
Explanation:
a.
Original equation:
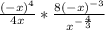
So (-x)^4 can be seen as (-x * -x) * (-x * -x), which becomes x^2 * x^2 = x^4, the negatives cancel out of the degree is even. So it becomes:
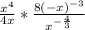
Cancel out one of the x's on the left fraction:
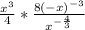
Rewrite the exponent in the numerator:
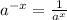
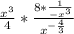
Simplify the numerator:
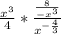
Keep numerator, change division to multiplication, flip the denominator:
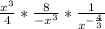
multiply the denominator using the exponent identity:
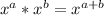
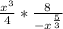
Multiply the numerators and denominators:
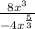
Use the fact that:
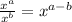 to divide the x^3 and x^(5/3) and divide the 4 by the -8
to divide the x^3 and x^(5/3) and divide the 4 by the -8
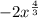
Rewrite the exponent using the exponent identity:
![x^{(a)/(b)} = \sqrt[b]{x^a}=\sqrt[b]{x}^a](https://img.qammunity.org/2023/formulas/mathematics/high-school/lub1ggimhkjioedg9mxfmj4jaag2349yxq.png)
![-2\sqrt[3]{x^4}](https://img.qammunity.org/2023/formulas/mathematics/high-school/8mga2pik06bp4vqvdnn4eilwuu3ug177up.png)
Rewrite as two radicals:
![\sqrt[n]{a} * \sqrt[n]{b} = \sqrt[n]{ab}](https://img.qammunity.org/2023/formulas/mathematics/high-school/mr1y7bherwumg99mnb4447cwr2mpmzz5z1.png)
![-2\sqrt[3]{x^3} * \sqrt[3]{x}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ygp90ql6hhuo1h6brjygfu4odriqet5p27.png)
Simplify:
![-2x\sqrt[3]{x}](https://img.qammunity.org/2023/formulas/mathematics/high-school/jvef05qd9r377gwhjwhlsg6htg9a9yglj9.png)
b.
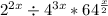
Rewrite the 4 as 2^2
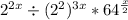
Use the exponent identity:
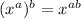
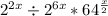
Use the exponent identity:
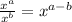
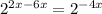
Rewrite this part using the definition of a negative exponent:
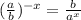 .
.
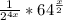
Multiply:
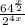
rewrite 64 as 2^6
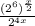
Use the identity:
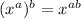
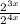
Use the identity:
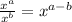

rewrite using the definition of a negative exponent: