The calculated sum of the series
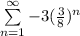 to infinity is (a) -9/5
to infinity is (a) -9/5
How to determine the sum of the series to infinity
From the question, we have the following parameters that can be used in our computation:
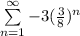
Set n = 1 to calculate the first term, a
So, we have
a = -3 * 3/8
a = -9/8
The common ratio is the expression in bracket
So, we have
r = 3/8
The sum of the series to infinity is calculated as
Sum = a/(1 - r)
Substitute the known values into the equation
Sum = -9/8/(1 - 3/8)
Sum = -9/8/(5/8)
Evaluate
Sum = -9/5
Hence, the sum of the series to infinity is (a) -9/5