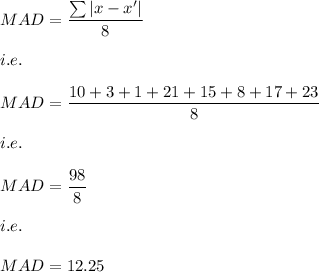Answer:
The mean absolute deviation of the data set is:
12.25
Explanation:
The data points are given as follows:
27, 34, 38, 16, 22, 45, 54, 60.
Total number of data points= 8
The mean of these data points is the average of the data points and is calculated as follows:

The absolute deviation of these data points is calculated as follows:
x Absolute deviation|x-x'|
27 |27-37|=10
34 |34-37|=3
38 |38-37|=1
16 |16-37|=21
22 |22-37|=15
45 |45-37|=8
54 |54-37|=17
60 |60-37|=23
Now, the mean of these absolute deviation i.e. Mean absolute deviation (MAD) is: