To solve this problem we use kinematics formulas.
to. What was the acceleration of the rocket during the first 16-s?
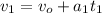
Where
 = speed after 16 s
= speed after 16 s
 = initial velocity = 0
= initial velocity = 0
 = acceleration during 16 s
= acceleration during 16 s

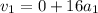
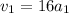
Now we use the formula for the position:
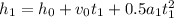
Where:
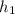 = position after 16 s
= position after 16 s
 = initial position = 0
= initial position = 0
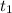 = 16 s
= 16 s
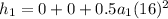
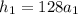
Then, we know that the altitude of the rocket after 20 s is 5100 meters.
Then we will raise the equation of the position of the rocket from the instant
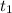 to
to
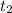
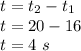
where:
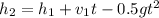
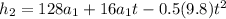

Now we clear
 .
.
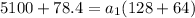
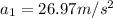
The aceleration is
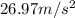
So:
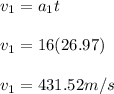
What is the speed of the rocket when it passes through a cloud at 5100 m above the ground?
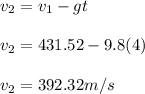
The speed is 392.32 m/s