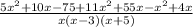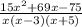Question

Add, subtract, multiply, or divide as indicated. List any restrictions for the variable(s) and simplify the answers when possible.

1) x-2 / x+5 + 3x / 2x-1

2) x+6 / x-6 - x^2 / x+6

3) x+9 / x-4 + x+2 / x^2-11x+28

4) x / x^2-64 + 11 / 2x^2+11x-40

5) 5 / x + 11 / x-3 - x-4 / x^2+2x-15

Answer 1

QUESTION 6

We want to simplify;


`(x - 2)/(x + 5) + (3x)/(2x - 1)`

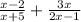
We collect LCM to get,




`= ((x - 2)(2x - 1) + 3x(x + 5))/((x + 5)(2x - 1))`




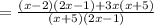
Expand the numerator to get;


`= \frac{2 {x}^(2) - x - 4x + 2+ 3 {x}^(2) + 15x}{(x + 5)(2x - 1)}`



`= \frac{2 {x}^(2) +3 {x}^(2)- x - 4x +15x + 2 }{(x + 5)(2x - 1)}`



`= \frac{5{x}^(2) + 10x + 2 }{(x + 5)(2x - 1)}`


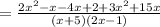
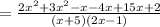
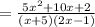
QUESTION 7


The given expression is

`(x + 6)/(x - 6) - \frac{ {x}^(2) }{x + 6}`



`= \frac{(x + 6)(x - 6) - {x}^(2)(x - 6) }{(x - 6)(x + 6)}`


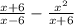
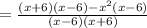
Expand the bracket to obtain,


`= \frac{{x}^(2) - 36 - {x}^(3) + 6 {x}^(2) }{(x - 6)(x + 6)}`

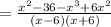
This simplifies to


`= \frac{ - {x}^(3) + 7{x}^(2) - 36 }{(x - 6)(x + 6)}`


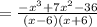
QUESTION 8


We want to simplify


`(x + 9)/(x - 4) + \frac{x + 2}{ {x}^(2) - 11x + 28 }`

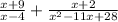
Let us factor the denominator of the fraction first.




`= (x + 9)/(x - 4) + \frac{x + 2}{ {x}^(2) - 7x - 4x+ 28 }`





`= (x + 9)/(x - 4) + (x + 2)/( x(x - 7) - 4(x - 7))`




`= (x + 9)/(x - 4) + (x + 2)/( (x - 7)(x- 4))`



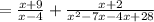
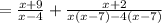
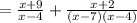
We collect LCM to obtain;



`= ((x + 9)(x - 7) + (x + 2))/( (x - 7)(x- 4)) .`


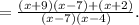
We expand brackets to get;


`= \frac{ {x}^(2) - 7x + 9x - 63+ x + 2}{ (x - 7)(x- 4)} .`


`= \frac{ {x}^(2) + 3x - 61}{ (x - 7)(x- 4)} .`



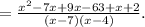
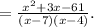
QUESTION 9

The given expression is


`\frac{x}{ {x}^(2) - 64} + \frac{11}{2 {x}^(2) + 11x - 40}`




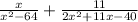
We factor the numerator of the second fraction to get,



`\frac{x}{ {x}^(2) - {8}^(2) } + \frac{11}{2 {x}^(2) + 16x - 5x- 40}`




`= \frac{x}{ {x}^(2) - {8}^(2) } + (11)/(2 x(x + 8) - 5(x + 8))`


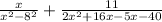
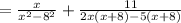
This implies that,


`= (x)/( (x - 8)( x + 8)) + (11)/((2 x - 5)(x + 8)) .`


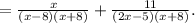
We collect LCM to get,


`= (x(2x - 5) + 11(x - 8))/((2 x - 5)(x + 8)(x - 8))`



`= \frac{2 {x}^(2) - 5x + 11x - 88}{(2 x - 5)(x + 8)(x - 8)}`



`= \frac{2 {x}^(2) + 6x - 88}{(2 x - 5)(x + 8)(x - 8)}`

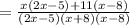
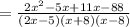
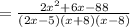
QUESTION 10

The given expression is


`(5)/(x) + (11)/(x - 3) - \frac{x - 4}{ {x}^(2) + 2x - 15}`


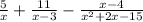
We factor the denominator to obtain:




`(5)/(x) + (11)/(x - 3) - (x - 4)/( (x - 3)(x + 5))`


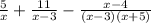
We collect LCM to get;


`(5(x - 3)(x + 5) + 11x(x + 5) - x(x - 4))/( x(x - 3)(x + 5))`

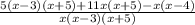
We expand brackets to get,



`\frac{5 {x}^(2) + 10x - 75 + 11 {x}^(2) + 55x- {x}^(2) + 4x}{ x(x - 3)(x + 5)}`



`\frac{15 {x}^(2) + 69x - 75 }{ x(x - 3)(x + 5)}`