Question

Solve: (1/4)^3z-1=16^z+2x64^z-2

Answer 1

Same thing again Apply the same rule

Answer 2

Value of z is 3/8.

Explanation:

Given:

`((1)/(4))^(3z-1)=16^(z+2)*64^(z-2)`

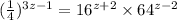
We need to solve the given expression.

Consider,

`((1)/(4))^(3z-1)=16^(z+2)*64^(z-2)`

`((1)/(2^2))^(3z-1)=(2^4)^(z+2)*(2^6)^(z-2)`

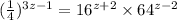
Now, using law of exponent
`(x^a)^b=x^(ab)`

`(((1)/(2))^2)^(3z-1)=(2)^(4(z+2))*(2)^(6(z-2))`

`((1)/(2))^(2(3z-1))=2^(4(z+2))*2^(6(z-2))`

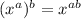
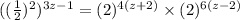
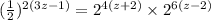
Now using Result of Exponent on LHS
`x^(-a)=((1)/(x))^a`

`2^(-2(3z-1))=2^(4(z+2))*2^(6(z-2))`

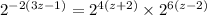
Now using another law of exponent on RHS,
`x^a* a^b=x^(a+b)`

`2^(-2(3z-1))=2^(4(z+2)+6(z-2))`

`2^(2-6z)=2^(4z+8+6z-12)`

`2^(2-6z)=2^(10z-4)`

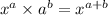
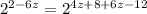
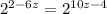
By comparing Exponent of both sides, we get

2 - 6z = 10z - 4

2 + 4 = 10z + 6z

16z = 6

z = 6/16

z = 3/8

Therefore, Value of z is 3/8.