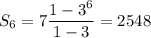Question

What is the sum of the geometric series in which a1 = 7, r = 3, and an = 1,701?

Hint: cap s sub n equals start fraction a sub one left parenthesis one minus r to the power of n end power right parenthesis over one minus r end fraction comma r ≠ 1, where a1 is the first term and r is the common ratio

Answer 1

My best interpretation of this is that you're given a geometric progression consisting of
`n` terms, the first of which is
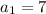`a_1=7` and the last of which is
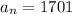`a_n=1701`. (So we don't actually know right away how many terms there are.) The common ratio between terms is
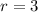`r=3`. You want to find the sum of all
`n` terms.

In a geometric progression, the
`k`-th term is determined by the previous term according to

`a_k=ra_(k-1)`

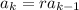
Starting with
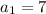`a_1=7`, we find

`a_2=3a_1=21`

`a_3=3a_2=3^2a_1=63`

`a_4=3a_3=3^3a_1=189`

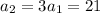
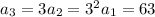
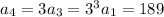
and so on. The general pattern for the
`k`-th term is then

`a_k=3^(k-1)a_1=7\cdot3^(k-1)`

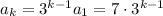
The last term in the sequence is
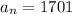`a_n=1701`, so

`1701=7\cdot3^(n-1)\implies 243=3^5=3^(n-1)\implies n=6`

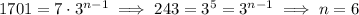
The sum of these
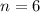`n=6` terms is given by

`S_6=\displaystyle\sum_(k=1)^6a_k=a_1+a_2+\cdots+a_6`

`S_6=a_1+ra_1+r^2a_1+\cdots+r^5a_1`

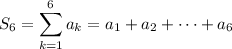
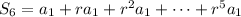
Notice that

`rS_6=ra_1+r^2a_1+r^3a_1+\cdots+r^6a_1`

`\impleis S_6-rS_6=a_1-r^6a_1`

`\implies(1-r)S_6=a_1(1-r^6)`

`\implies S_6=a_1(1-r^6)/(1-r)`

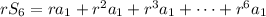
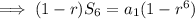
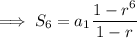
With
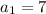`a_1=7` and
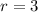`r=3`, we get a sum of

`S_6=7(1-3^6)/(1-3)=2548`