Question

36x2 + 49y2 = 1,764 The foci are located at:

A) (-√13, 0) and (√13,0)
B) (0, -√13) and (0,√13)
C) (-1, 0) and (1, 0)

Answer 1

The answer is A) (-√13, 0) and (√13,0)

Explanation:

Given equation is 36x^2 + 49y^2 = 1,764

We have to find the foci

The above equation can be written as
`(x^2)/(49)+(y^2)/(36)=1`

This equation is of the form of ellipse whose standard equation can be written as
`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

where a represents the radius of the major axis and b represents the radius of the minor axis of the ellipse.

By comparing the above two equations, we get

a=7, b=6, h=0 and k=0

The foci of ellipse are (h+c,k) and (h-c,k)

c is the distance from the center to a focus which can be calculated as

`\sqrt(a^2-b^2)=\sqrt(7^2-6^2)=\sqrt13`

Substitute the values to find foci, we get

`(0+\sqrt13,0)` and
`(0-\sqrt13,0)`

⇒
`(\sqrt13,0)` and
`(-\sqrt13,0)`

Answer 2

Option (A) is correct.

Foci of given equation located at (-√13, 0) and (√13,0)

Explanation:

Consider the given equation
`36x^2+49y^2=1764`

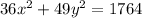
We have to find the foci for the above equation,

First divide whole equation by 1764,

`\Rightarrow (36)/(1764)x^2+(49)/(1764)y^2=(1764)/(1764)`

`\Rightarrow (1)/(49)x^2+(1)/(36)y^2=1`

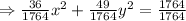
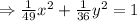
Since, both terms are positive so it is an equation of ellipse, a > b,

So it is a horizontal ellipse,

`( (x-h)^2)/(a^2)+ ( (y-k)^2)/(b^2)=1`

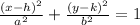
With center at (h , k ) and foci ( h±c, k) where,
`c^2=a^2-b^2`

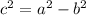
Given equation ,
`(1)/(49)x^2+(1)/(36)y^2=1`

`(1)/(7^2)x^2+(1)/(6^2)y^2=1` ,

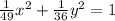
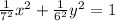Comparing a= 7 , b = 6 , h = k = 0

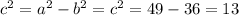`c^2=a^2-b^2=c^2=49-36=13` thus c = ±√13

Thus, foci is ( h±c, k) = (0 ±√13 ,0)

Thus, Foci of given equation located at (-√13, 0) and (√13,0)

Thus, option (A) is correct.