Answer:
The maximum power is produced at current = 4 A
Explanation:
Given:
The power generated by an electrical circuit (in watts) is modeled as a function of current as:

To find the current that will produce the maximum power.
Solution:
The function can be simplified using distribution.
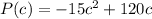
We know that the power will be maximum at the point where the slope of the equation will be = 0 i.e. parallel to x-axis.
Finding the slope of the function using derivative.
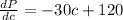
We will equate the slope = 0 to get the current for maximum power.
Thus, we have:
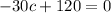
Subtracting both sides by 120.

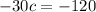
Dividing both sides by -30.

∴
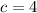
Thus, the maximum power is produced at current = 4 A