Question

Candice uses the function f(t)=t+100−−−−−−√ to model the number of students in her after-school program. The variable t represents days and f(t) represents the number of students. How many days does it take for there to be 15 students in her program? A. 225 days B. 125 days C. 325 days D. 115 days

Answer 1

Let's solve the problem step by step.

1. We know that Candice uses the function \( f(t) = \sqrt{t + 100} \), where \( t \) is the number of days and \( f(t) \) is the number of students.

2. We want to find the number of days (\( t \)) it takes for there to be 15 students in her program. So, we set \( f(t) \) equal to 15:
\[ f(t) = 15 \]

3. Now, we can substitute the expression of \( f(t) \) into the equation, which gives us:
\[ \sqrt{t + 100} = 15 \]

4. To solve for \( t \), we need to square both sides of the equation to get rid of the square root:
\[ (\sqrt{t + 100})^2 = 15^2 \]

5. Squaring both sides yields:
\[ t + 100 = 225 \]

6. Now we just solve for \( t \) by subtracting 100 from both sides:
\[ t = 225 - 100 \]
\[ t = 125 \]

Thus, it takes 125 days for there to be 15 students in Candice's after-school program. The correct answer is B. 125 days.

Answer 2

Option B is correct.

125 days does it take for there to be 15 students in her program.

Explanation:

As per the statement:

Candice uses the function:

`f(t) = √(t+100)` [1]

where variable t represents the days and f(t) represents the number of studemts.

We have to find how many days does it take for there to be 15 students in her program.

⇒f(t) = 15 students

then substitute in [1] we get;

`15 = √(t+100)`

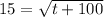
Squaring both sides we have;

`225 = t+100`

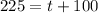
Subtract 100 from both sides we get;

`225-100= t+100-100`

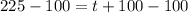
Simplify:

`125 = t`

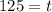
Therefore, 125 days does it take for there to be 15 students in her program.