Question

For the sequence
`a_(n) = 2n/(n+1)`, what is the value of
`a_(10)`

Answer 1

330

Explanation:

We are given the following arithematic sequence and we are to find the 10th term in this sequence:

`a_n = \frac {2n} {( n + 1 )}`

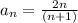
where
`n` is the number of the term.

To find the 10th term, we will simply substitute '10' in place of n in the above given formula:

`a_n = \frac {2n} {( n + 1 )}`

`a_(10) = \frac {2(10)} {( 10 + 1 )} =30(11) = 330`

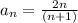
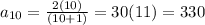
Therefore, the 10th term of this sequence is 330.

Answer 2

`a_(10)=(20)/(11)`

Explanation:

The formula for nth term of a the sequence is given as
`a_n=(2n)/(n+1)`

Finding the 10th term means finding
`a_(10)`, which means to plug in 10 into n, in the nth term formula.

`a_(10)=(2(10))/((10)+1)=(20)/(11)`