Answer: 11378.583 feet (approx)
Explanation:
Let from the foot of the line that shows the distance of the plane from the road the distance of first car is x feet and the distance of second car is y feet,
Thus, by the below figure,
We can write,
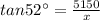
⇒

⇒
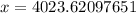
Similarly, by the below diagram,
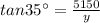
⇒
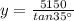
⇒
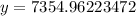
Thus, the total distance between the car = x + y = 4023.62097651 + 7354.96223472= 11378.5832112≈11378.583 feet