Question

△ABC is similar to △XYZ. Also, side AB measures 6 cm, side BC measures 18 cm, and side XY measures 12 cm.

What is the measure of side YZ ?



Enter your answer in the box.

Answer 1

Answer: YZ=36 cm

Explanation:

Given: △ABC is similar to △XYZ.

Side AB =6 cm, side BC = 18 cm, and side XY=12 cm.

We know that if two triangles are similar then their sides are proportional.

Therefore, if △ABC is similar to △XYZ.

Then,
`(AB)/(XY)=(BC)/(YZ)\\`

`\\\Rightarow(6)/(12)=(18)/(YZ)\\\Rightarrow\ YZ=(18*12)/(6)\\\Rightarrow\ YZ=36\ cm`

Answer 2

value of sides YZ is 36 cm

Explanation:

Similar triangles states that the length of the corresponding sides are in proportion.

Given that: ΔABC is similar to ΔXYZ

then;

Corresponding sides are in proportion i.e

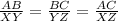`(AB)/(XY)=(BC)/(YZ)=(AC)/(XZ)` .....[1]

As per the statement:

side AB = 6 cm, side BC =18 cm and side XY = 12 cm.

Substitute these in [1] to solve for side YZ;

`(6)/(12)= (18)/(YZ)`

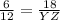
or

`(1)/(2) = (18)/(YZ)`

By cross multiply we have;

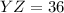`YZ = 36` cm

Therefore, the value of sides YZ is 36 cm