Answer: The answer is 30.56 feet.
Step-by-step explanation: As shown in the attached figure, Sara is flying a kite at the park with angle of elevation from Sara to kite in the sky, ∠BAC = 53° and length of the string, AC = 32 feet. Sara is 5 feet tall. We need to find the height of the kite from the ground.
Fro the right angled-triangle ABC, we have
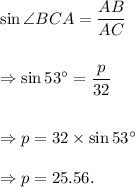
Since Sara is 5 feet tall, so the height of the kite from the ground is
AD = AB + BD = p + 25.56 = 5 + 25.56 = 30.56 feet.
Thus, the answer is 30.56 feet.