Question

The statement tan theta= -12/5, csc theta=-13/12, and the terminal point determained by theta is in quadrant two

Answer 1

cannot be true because csc theta is greater than zero in quadrant 2

Explanation:

apex users good luck

Answer 2

tan (theta)
`=(-12)/(5)`
`=\frac{\text{Perpendicular}}{\text{Base}}`

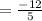
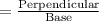
Cosec(theta)
`=(-13)/(12)`
`=\frac{\text{Hypotenuse}}{\text{Altitude}}`

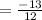
In right Triangle,

using Pythagoras theorem

(Hypotenuse)²= (Base)² + (Altitude)²

⇒ (Hypotenuse)²= (12)² + (5)²

⇒Hypotenuse= √(144 +25)

⇒Hypotenuse= 13 cm

As, the value of tan(theta)
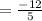`=(-12)/(5)` is true if Theta lies in Second Quadrant, but it is not true for Cosec(theta)
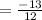`=(-13)/(12)` ,if theta lies in second Quadrant, because value of Cosec(theta) is positive in second Quadrant ,irrespective of fact that Terminal side lies in Second Quadrant.

So, The statement tan (theta)= -12/5, and Cosec (theta)=-13/12, and the terminal point determined by theta is in quadrant two is Incorrect.