Answer: 20.8 units
Explanation:
From the given picture, it can be seen that the radius of the circle r= 12 units
The distance from chord to the center of the circle a= 6 units
We know that in a circle , the perpendicular line from the center of the circle bisect the chord.
Using Pythagorean theorem of right triangle , we get
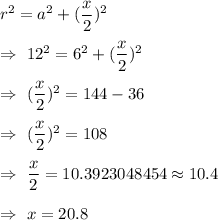
The value of x = 20.8 units.