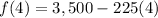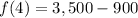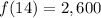Answer:
The water level is falling.
The initial level of water in the pool was 3,500 units
The water was 2,600 units high after 4 hours.
Explanation:
The given function that models the water level is
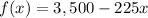
where
 represents time in hours.
represents time in hours.
The function represents a straight line that has slope
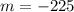
Since the slope is negative, it means the water level is falling.
The initial level of water in the pool can found when we put
 into the function.
into the function.

 , hence the initial level is 3,500.
, hence the initial level is 3,500.
To determine the level of water in the pool after 14 hours, we put
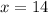 into the equation to get;
into the equation to get;


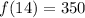
To determine the water level after 4 hours we put