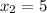Answer:
 and
and
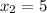
Explanation:
Consider given system ,
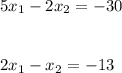
We have to solve for
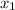 and
and
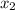
In matrix form,
![\left[\begin{array}{cc}5&-2\\2&-1\end{array}\right]\left[\begin{array}{c}x_1\\x_2\end{array}\right] =\left[\begin{array}{c}-30\\-13\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/high-school/c0i6ng97zc4098e0x4matc5stezornkkor.png)
then this is in form of AX = b,
A=
![\left[\begin{array}{cc}5&-2\\2&-1\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/high-school/u6icj977drkijx8s4ayysnilajvxq5xctr.png)
X=
![\left[\begin{array}{c}x_1\\x_2\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/high-school/s4tasdn3sbo5nji22qdgad80xqdu9wozd7.png)
b=
![\left[\begin{array}{c}-30\\-13\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/high-school/8f85zv7ec5bu3r7lag09ci02zszzyt2fvj.png)
Pre-multiply by
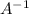 both side, we get,
both side, we get,
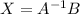 ..............(1)
..............(1)
First finding inverse of A ,
![\mathrm{Find\:2x2\:matrix\:inverse\:according\:to\:the\:formula}:\quad \begin{pmatrix}a\:&\:b\:\\ c\:&\:d\:\end{pmatrix}^(-1)=\frac{1}{\det \begin{pmatrix}a\:&\:b\:\\ c\:&\:d\:\end{pmatrix}}\begin{pmatrix}d\:&\:-b\:\\ -c\:&\:a\:\end{pmatrix}]()
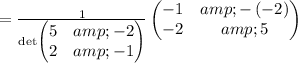
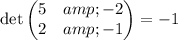
Thus, inverse of A is ,
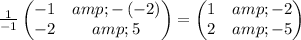
Now substitute
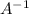 in (1) , we get,
in (1) , we get,
![\left[\begin{array}{c}x_1\\x_2\end{array}=\left[\begin{array}{cc}1&-2\\2&-5\end{array}\right]\left[\begin{array}{c}-30\\-13\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/high-school/l98on3qa99w271lva9h9et9ydhxt0rzi0l.png)
Multiply , we get,
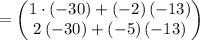
![\left[\begin{array}{c}x_1\\x_2\end{array}\right]=\left[\begin{array}{c}-4\\5\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/high-school/fu05n7qkvn3hjwvjqz1shyqkehoaptin2q.png)
Thus,
 and
and