Question

Monthly water bills for a city have a mean of $108.43 and a standard deviation of $36.98. Find the probability that a randomly selected bill will have an amount greater than $173, which the city believes might indicate that someone is wasting water. Would a bill that size be considered unusual?

Answer 1

The probability that a randomly selected bill will have an amount greater than $173 is 0.04006.

No, a bill with $173 can not be considered unusual.

Explanation:

We have been given that monthly water bills for a city have a mean of $108.43 and a standard deviation of $36.98.

First of all, we will find z-score of data point 173 using z-score formula.

`z=(x-\mu)/(\sigma)`, where,

`z=\text{Z-score}`

`x=\text{Random sample score}`

`\mu=\text{Mean}`

`\sigma=\text{Standard deviation}`

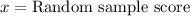
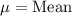
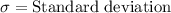
Substitute the given values:

`z=(173-108.43)/(36.98)`

`z=(64.57)/(36.98)`

`z=1.75`

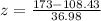
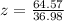
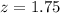
Now, we will use formula
`P(z>a)=1-P(z<a)` as:

`P(z>1.75)=1-P(z<1.75)`

From normal distribution table, we will get:

`P(z>1.75)=1-0.95994`

`P(z>1.75)=0.04006`

Therefore, the probability that a randomly selected bill will have an amount greater than $173 would be 0.04006 or 4.001%.

Since z-scores lower than -1.96 or higher than 1.96 are considered unusual. As the bill with size $173 has z-score of 1.75, therefore, a bill with size $173 can not be considered unusual.

Answer 2

The bill size can be considered usual.

Explanation:

Mean (μ) = $108.43

Standard deviation (σ) = $36.98

Now, consider the distribution to be normal distribution :

`P(Z=(X-\mu)/(\sigma)>(a-\mu)/(\sigma))=P(Z>(173-108.43)/(36.98))\\\\\implies P(Z>1.75)`

Now, finding values of z-score from the table. We get,

P(Z > 1.75) = 0.9599

⇒ 95.99%

So, only 4.01 % of the people in the city wastes water.

Hence, the bill size can be considered usual.