Answer:
The graph of an exponential function of the form y = f(x) = aˣ passes through the points (0, 1) and (1, a). The graph lies above the x-axis.
Explanation:
The given function is

Put x=0 in the given function,
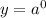
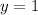
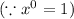
Put x=1 in the given function,
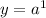
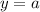
Therefore graph of an exponential function of the form y = f(x) = aˣ passes through the points (0, 1) and (1, a).
It is an positive exponential function, therefore the value of function will always remains positive. So, the graph lies above the x-axis.