Question

Special right triangles.

Answer 1

QUESTION 9

The given right angle triangle has its two legs equal to
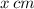`x\:cm` and the hypotenuse is
`2\:units`.

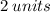Using the Pythagoras theorem, we have

`x^2+x^2=2^2`

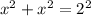
This implies that;

`2x^2=2^2`

`2x^2=4`

`x^2=2`

`x=√(2)`

`x=1.414`

`x\approx1.4\:units`

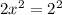
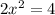
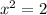
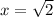
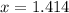
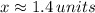
QUESTION 10

The given right angle triangle has its two legs equal to
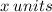`x\:units` and the hypotenuse is
`7\:units`.

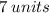Using the Pythagoras theorem, we have

`x^2+x^2=7^2`

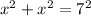
This implies that;

`2x^2=7^2`

`2x^2=49`

`x^2=24.5`

`x=√(24.5)`

`x=4.95\:units`

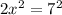
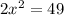
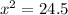
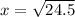
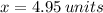
QUESTION 11

Sam divided the square backyard into two sections along the 40ft diagonal.

Let one of the sides of the garden be
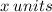`x\:units`, then the other side of the garden is also
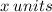`x\:units` since it was a square backyard.

The diagonal is the hypotenuse which is 40ft and the two legs are
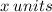`x\:units` each.

Applying the Pythagoras Theorem, we have;

`x^2+x^2=40^2`

`2x^2=1600`

`x^2=800`

`\Rightarrow x=√(800)`

`\Rightarrow x=28.28`

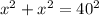
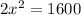
The length of one side of the garden is approximately 28cm.

QUESTION 12

The hypotenuse of Nicole's right triangular support is 92cm long.

It was given that the two lengths of the triangular support are of equal length.

Let the two lengths of the triangular support be
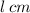`l\:cm` each.

We then apply the Pythagoras theorem to obtain;

`l^2+l^2=92^2`

`\Rightarrow 2l^2=8464`

`\Rightarrow l^2=4232`

`\Rightarrow l=√(4232)`

`\Rightarrow l=65.05cm`

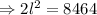
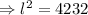
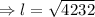
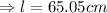
Therefore Nicole needs
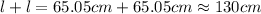`l+l=65.05cm+65.05cm\approx130cm` of wood to complete the support.

The correct answer is A.

QUESTION 13

A 45-45-90 triangle is an isosceles right triangle.

Let the length of the two legs be
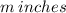`m\:inches` each.

It was given that the hypotenuse of this triangle is
`12\:inches`.

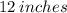Applying the Pythagoras Theorem, we have;

`m^2+m^2=12^2`

`\Rightarrow 2m^2=144`

`\Rightarrow m^2=72`

`\Rightarrow m=√(72)`

`\Rightarrow m=8.49`

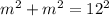
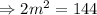
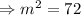
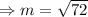
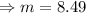
The length of one leg of the hypotenuse is approximately 8.5 inches to 1 decimal place.

QUESTIONS 14.

It was given that the distance from home plate to first base is 90 feet.

Since the baseball field form a square, the length of the baselines are all 90ft.

We want to calculate the distance from home plate to 2nd base,which is the diagonal of the square baseball field.

Let this distance be
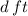`d\:ft`, then using the Pythagoras theorem;

`d^2=90^2+90^2`

`d^2=8100+8100`

`d^2=16200`

`\:d=√(16200)`

`\:d=127.279`

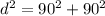
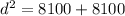
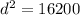
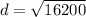
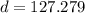
Therefore the distance from home plate to second base is 127 ft to the nearest foot.

QUESTION 15.

The distance from third base to first base is also 127 ft to the nearest foot.

The reason is that the diagonals of a square are equal in length.