Question

Special right triangles

Answer 1

Answer: The answers are given below.

Step-by-step explanation: The calculations are as follows.

(1) We have in the given right-angled triangle,

`\tan 30^\circ=(10)/(x)\\\\\Rightarrow (1)/(\sqrt3)=(10)/(x)\\\\\Rightarrow x=10\sqrt3,`

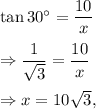
and

`y^2=(10)^2+x^2=100+(10\sqrt3)^2=100+300=400\\\\\Rightarrow y=20.`

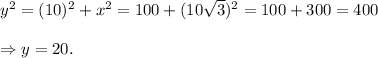
∴ x = 10√3 and y = 20.

(2) We have in the given right-angled triangle,

`\cos 60^\circ=(2)/(x)\\\\\Rightarrow (1)/(2)=(2)/(x)\\\\\Rightarrow x=4,`

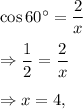
and

`y^2=x^2-2^2=16-4=12\\\\\Rightarrow y=2\sqrt3.`

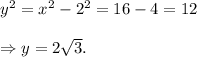
∴ x = 4 and y = 2√3.

(3) We have in the given right-angled triangle,

`\cos 30^\circ=(7)/(y)\\\\\Rightarrow (\sqrt3)/(2)=(7)/(y)\\\\\Rightarrow y=(14\sqrt3)/(3),`

and

`\sin 30^\circ=(7)/(x)\\\\\Rightarrow (1)/(2)=(7)/(x)\\\\\Rightarrow x=14.`

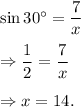
∴ x = 14 and y = 14√3.

(4) We have in the given right-angled triangle,

`\sin 30^\circ=(x)/(6)\\\\\Rightarrow (1)/(2)=(x)/(6)\\\\\Rightarrow x=3,`

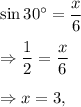
and

`\cos 30^\circ=(y)/(6)\\\\\Rightarrow (\sqrt3)/(2)=(y)/(6)\\\\\Rightarrow y=3\sqrt3.`

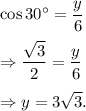
∴ x = 3 and y = 3√3.

(5) We have in the given right-angled triangle,

`\sin 30^\circ=(y)/(10)\\\\\Rightarrow (1)/(2)=(y)/(10)\\\\\Rightarrow y=5,`

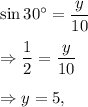
and

`\cos 30^\circ=(x)/(6)\\\\\Rightarrow (\sqrt3)/(2)=(x)/(10)\\\\\Rightarrow y=5\sqrt3.`

∴ x = 5 and y = 5√3.

(6) We have in the given right-angled triangle,

`\sin 30^\circ=(x)/(8)\\\\\Rightarrow (1)/(2)=(x)/(8)\\\\\Rightarrow x=4,`

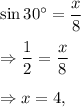
and

`\cos 30^\circ=(y)/(8)\\\\\Rightarrow (\sqrt3)/(2)=(y)/(8)\\\\\Rightarrow y=4\sqrt3.`

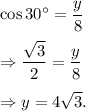
∴ x = 4 and y = 4√3.

(7) We have in the given right-angled triangle,

`\cos 30^\circ=(7\sqrt3)/(y)\\\\\Rightarrow (\sqrt3)/(2)=(7\sqrt3)/(y)\\\\\Rightarrow y=14,`

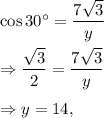
and

`\sin 30^\circ=(x)/(y)\\\\\Rightarrow (1)/(2)=(x)/(14)\\\\\Rightarrow x=7.`

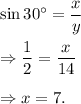
∴ x = 7 and y = 14.

(8) We have in the given right-angled triangle,

`\cos 30^\circ=(6\sqrt3)/(y)\\\\\Rightarrow (\sqrt3)/(2)=(6\sqrt3)/(y)\\\\\Rightarrow y=12`

and

`\sin 30^\circ=(x)/(y)\\\\\Rightarrow (1)/(2)=(x)/(12)\\\\\Rightarrow x=6`

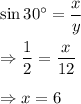
∴ x = 6 and y = 12.

(9) We have in the given right-angled triangle,

`\cos 30^\circ=(\sqrt3)/(y)\\\\\Rightarrow (\sqrt3)/(2)=(\sqrt3)/(y)\\\\\Rightarrow y=2`

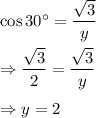
and

`\sin 30^\circ=(x)/(y)\\\\\Rightarrow (1)/(2)=(x)/(2)\\\\\Rightarrow x=4.`

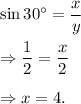
∴ x = 4 and y = 2.

Thus, all are completed.