Answer:
94 cents
Explanation:
Using eight coins, the maximum is
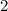 dollars, so we need to find a value lower than that. If we imagine
dollars, so we need to find a value lower than that. If we imagine
 pennies, and add one to that, since we can make any value under
pennies, and add one to that, since we can make any value under
 cents, we will get
cents, we will get
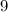 cents. We can make this with a nickel, so we also need to be out of range of nickels, so we should try
cents. We can make this with a nickel, so we also need to be out of range of nickels, so we should try
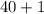 . We can make this with dimes, so we should try
. We can make this with dimes, so we should try
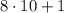 .
.
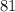 can be made with quarters, so we should try
can be made with quarters, so we should try
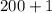 and get
and get
 cents. But, we cannot forget about subtracting from these values. If we try
cents. But, we cannot forget about subtracting from these values. If we try
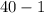 , we get
, we get
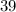 , which is made with dimes. Trying
, which is made with dimes. Trying
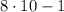 makes
makes
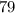 , but if we keep moving it down to the nearest multiple of
, but if we keep moving it down to the nearest multiple of
 , or a quarter, we will get
, or a quarter, we will get
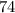 .
.
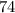 can be made with
can be made with
 coins though, but if we take it away again down to
coins though, but if we take it away again down to
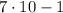 , we get
, we get
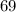 . This looks hopeful. This has
. This looks hopeful. This has
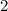 quarters,
quarters,
 dime,
dime,
 nickel, and four pennies. If we keep trying and move it down to
nickel, and four pennies. If we keep trying and move it down to
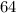 , we can still make it. If we keep moving down till we get to the LCM of the values, we get
, we can still make it. If we keep moving down till we get to the LCM of the values, we get
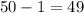 . Making this does works, so now we know it is between
. Making this does works, so now we know it is between
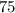 cents and
cents and
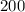 cents. Trying the nearest multiple of
cents. Trying the nearest multiple of
 minus
minus
 , we get
, we get
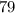 . This obviously works, so we need to get away from the multiple of
. This obviously works, so we need to get away from the multiple of
 . Trying
. Trying
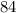 , we get
, we get
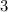 ,
,
 , and
, and
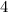 coin types, so this works. Now try
coin types, so this works. Now try
 . This is
. This is
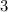 quarters,
quarters,
 dime, and four pennies. Trying
dime, and four pennies. Trying
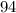 , we get
, we get
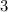 quarters,
quarters,
 dime,
dime,
 nickel, and four pennies.There is nothing lower than this, so we have found it! :D This took me very long to do, and even I learned something from doing your super hard question! Thanks for the workout!
nickel, and four pennies.There is nothing lower than this, so we have found it! :D This took me very long to do, and even I learned something from doing your super hard question! Thanks for the workout!
EDIT: Oops! I did less than or equal to! But you can use the same logic to do it again!