Answer:
Hello! the answer to this question is 30.
Explanation:
To solve for the quotient, we have to convert the mixed number to an improper fraction:
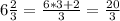
When dividing fractions, we have to flip the divisor to its reciprocal. When doing so, the divisor
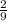 becomes
becomes
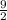 .
.
Now that we have the reciprocal, the operation will change from division to multiplication. We can take the final steps to solve the problem:
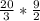
This leaves you with a result
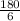 . This can further be simplified by doing 180 ÷ 6 to get 30.
. This can further be simplified by doing 180 ÷ 6 to get 30.
Therefore, the quotient is 30.