Question

Suppose you want to transform the graph of the function y=tan(x+pi/4)-1 into the graph of the function y=-tan(x+pi/2)+1 which transformations should you perform.

A) Reflect the graph of the first function across the x-axis, translate it pi/4 units to the left, and translate it 2 units up.
B) Reflect the graph of the first function across the x-axis, translate it pi/4 units to the right, and translate it 2 units up.
C) Reflect the graph of the first function across the line y = -1, translate it pi/4 units to the left, and translate it 2 units up.
D) Reflect the graph of the first function across the line y = -1, translate it pi/4 units to the right, and translate it 2 units up.

Answer 1

a

Explanation:

Answer 2

A) Reflect the graph of the first function across the x-axis, translate it pi/4 units to the left, and translate it 2 units up

Explanation:

We are given

parent function as

`y=tan(x+(\pi)/(4))-1`

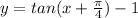
and new function as

`y=-tan(x+(\pi)/(2))+1`

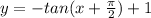
We can also write as new function as

`y=-tan(x+(\pi)/(4)+(\pi)/(4))+1+1-1`

`y=-tan(x+(\pi)/(4)+(\pi)/(4))-1+2`

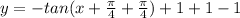
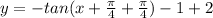
We can see that

x-value is added by pi/4

So, it is shifted left side pi/4

and y-value is added by 2 units

so, it moves 2 units upward

we can see that

y-value is multiplied by -1

so, it reflected about x-axis

so,

A) Reflect the graph of the first function across the x-axis, translate it pi/4 units to the left, and translate it 2 units up