Answer: Second Option is correct.
Explanation:
Since we have given that
In a parallelogram, the vector from one vertex to another vertex is (9,-2)
So, the co-ordinate of first vertex will be (9,0).
And the coordinate of second vertex will be (0,-2).
As we know the formula for "Distance between two coordinates":
So, The length of the side is given by
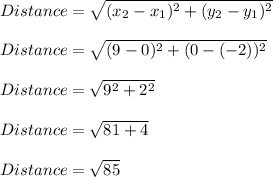
Hence, Second Option is correct.