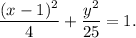Question

If the vertices of an ellipse are at (1, 5) and (1, -5) and (3, 0) is a point on the ellipse, what is the ellipse equation?

Answer 1

the answer is b.

Explanation:

Answer 2

`((x-1)^2)/(4)+(y^2)/(25)=1`

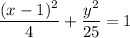
Explanation:

The equation of the ellipse is

`((x-x_0)^2)/(a^2)+((y-y_0)^2)/(b^2)=1,`

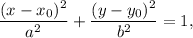
where
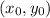`(x_0,y_0)` are the coordinates of the center.

If the vertices of an ellipse are at A(1, 5) and B(1, -5), then the center is the midpoint of the segment AB. Hence, the center has coordinates

`\left((1+1)/(2),(5+(-5))/(2)\right)=(1,0).`

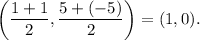
The coordinates of the vertices satisfy the equation:

`((1-1)^2)/(a^2)+((5-0)^2)/(b^2)=1\Rightarrow b^2=25.`

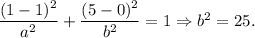
If (3, 0) is a point on the ellipse, then its coordinates satisfy the equation:

`((3-1)^2)/(a^2)+((0-0)^2)/(b^2)=1\Rightarrow a^2=4.`

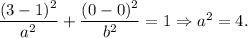
Therefore, the equation of the ellipse is

`((x-1)^2)/(4)+(y^2)/(25)=1.`