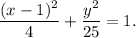Answer:
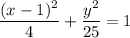
Explanation:
The equation of the ellipse is
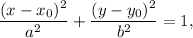
where
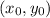 are the coordinates of the center.
are the coordinates of the center.
If the vertices of an ellipse are at A(1, 5) and B(1, -5), then the center is the midpoint of the segment AB. Hence, the center has coordinates
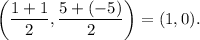
The coordinates of the vertices satisfy the equation:
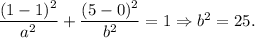
If (3, 0) is a point on the ellipse, then its coordinates satisfy the equation:
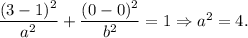
Therefore, the equation of the ellipse is