Question

Match the functions with correct transformation.

Question 1 options:

stretch by a factor of 4


shift to the left 3


shift up 3


compression by a factor of 4


shift to the right 1


shift to the left 1


compression by a factor of 1/2


reflection


stretch by a factor of 1/2


shift to the right 3


shift down 3

Functions
1.
f(x) = 3^x

2.
f(x) = |x-1| +3

3.
f(x) = √(x+3)

4.
f(x) = (x+1)²-3

5.
f(x) = 1/2x^2
6.
f(x) = 4|x|

Put the number of the function by the transformation

Answer 1

We are given the functions after applying some transformations.

It is required to find the corresponding transformations applied.

According to the options:

1. f(x) = -3^x

We see that, the function f(x) = 3^x is reflected across x-axis to obtain f(x) = -3^x

2. f(x) = |x-1| +3

We see that, the function f(x) = |x| is shifted 1 unit to the right and then 3 units up to obtain f(x) = |x-1| +3.

3.
`f(x) = √(x+3)`

We see that, the function
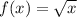`f(x) =√(x)` is shifted 3 units to the left to obtain
`f(x) = √(x+3)`.

4.
`f(x) = (x+1)^2-3`

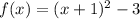
We see that, the function
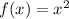`f(x)=x^(2)` is shifted 1 unit to the left and then 3 units downwards to obtain
`f(x) = (x+1)^2-3`.

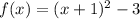5.
`f(x) =(1)/(2)x^(2)`

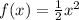
We get that, the function
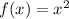`f(x)=x^(2)` is compressed by factor
`(1)/(2)` to obtain
`f(x) =(1)/(2)x^(2)`.

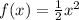6. f(x) = 4|x|

We get that, the function f(x) = |x| is stretched by factor of 4 to obtain f(x) = 4|x|