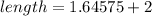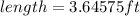Answer:
Exact dimensions:
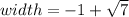

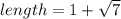
Approximate dimensions:

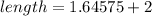
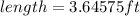
Explanation:
Let's assume width of rectangle is w ft
The length of a rectangular flower bed is 2ft longer than the width
so,
length =w+2
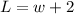
now, we can find area
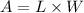
now, we can plug it

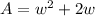
we are given area =6
so, we can set it equal
and then we can solve for w
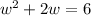
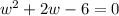
we can use quadratic formula


now, we can compare and find a,b and c
a=1 , b=2 , c=-6
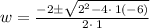
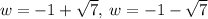
we know that dimension can never be negative
so, we will only consider positive value
Exact dimensions:
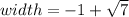

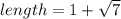
Approximate dimensions: