ANSWER
1.
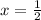
2.

QUESTION 1
The first sentence is
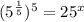 .
.
Recall that;
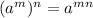
We simplify the left hand side by applying this property to get;
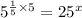 .
.
 .
.
We now rewrite the right hand side too in an index form to obtain;
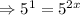
We now equate the exponents to get;
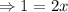 .
.
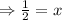
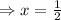 .
.
QUESTION 2
The second sentence is
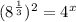
We simplify the left hand side first to get;
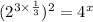

We now rewrite the left hand side too in index form to obtain;

We equate the exponents to get;

This implies that;

or
