Question

Which of the following statements about the function f (x) = sec(x) are true? Select all that apply

Answer 1

1. pi/2 and 3pi/2

2. f(x)=cotx

3. domain: -inf<x<inf, x does not equal pi/2+npi, where n is an integer

range: -inf<y<inf

4. f(x)=cotx and f(x)=secx

5. It is true, because the cosine function has a period of 2pi

6. f(x) has no zeros and f(x) has a period of 2pi

7. right pi/4

8. 4pi

9. It has an amplitude of 1/4 and it is a horizontal shift of the parent function pi/3 units left

10. the amplitude and the vertical shift

Explanation:

Just took the quiz

Answer 2

First option. f(x) has no zeroes

Second option. f(x) has a period of 2π.

Explanation:

1) The function sec(x) is the inverse of the cosine function:

`y=sec(x)=(1)/(cos(x) )`

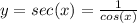
This function has no zeroes, because:

`y=sec(x)=(1)/(cos(x))`

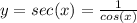
it can not be equal to zero

Then the first option is true.

2) As the secant function is the inverse of the cosine function, it has the same period 2π, then the second option is true.

3) The cosine function has an amplitude of 1, but the secant function does not, then the third option is false.

4) The secant function is symmetric about the y-axis, but not about the origin, then the fourth option is false.

5) The asymptotes of the secant funtion are where the cosine function is equal to zero, this is at integer multiples of π/2, then 5the fifth option is false.