Question

Which of the following trigonometric functions, restricted to 0

Answer 1

cot x and sec x

Explanation:

Given are 4 trignometric functions defined in the interval [0,\pi]

We are asked to identity the functions which can take values more than 1.

We have

`f(x)=sinx : f(x)= cos x`

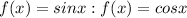
have values always between -1 and 1 for any value of x

Hence sinx and cosx cannot take values greater than 1.

`f(x) =cotx`

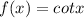
This value being ratio of cos to sin will become greater than 1 whenever cos >sin value.

SO this function can take values >1

`f(x)=secx`

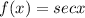
This function being reciprocal of cos function always can take values outside

(-1,1)

Hence this value can be greater than 1