Question

Triangle ABC and triangle DEG are similar right triangles. Which proportion can be used to show that the slope of AC is equal to the slope of DG?

A)
4 − (−7)
0 − 4
=
−1 − 10
4 − 8
B)
−4 − (−7)
0 − 4
=
4 − 8
−1 − (−10)
C)
0 − 4
−4 − (−7)
=
−1 − (−10)
−4 − 8
D)
0 − 4
−4 − (−7)
=
−4 − 8
−1 − (−10)

Answer 1

Option D is correct.

Slope of AC = Slope of DG

`(0-4)/(-4-(-7))=(-4-8)/(-1-(-10))`

Explanation:

Similar triangle states that if two triangles are similar then, their corresponding sides are in proportion.

As per the statement:

Triangle ABC and triangle DEG are similar right triangles.

By definition:

Corresponding sides are in proportion then;

`(AB)/(DE)=(BC)/(EG)=(AC)/(DG)`

From the graph:

The coordinate of A and C are:

A (-7, 4) and C(-4, 0)

Formula for slope is given by:

`\text{Slope} =(y_2-y_1)/(x_2-x_1)`

then;

`\text{Slope of AC} =(0-4)/(-4-(-7))`

The coordinates of D and G are:

D(-10, 8) and G(-1, -4)

then;

`\text{Slope of DG} =(-4-8)/(-1-(-10))`

Slope of AC = Slope of DG

`(0-4)/(-4-(-7))=(-4-8)/(-1-(-10))`

Answer 2

Option D is correct.

Explanation:

By looking at the graph attached, first look up the coordinates of the points A, C, D and G in order to find their required slopes.

Now, finding the coordinates of the points from the graph :

Coordinates of A = (-7,4)

Coordinates of C = (-4,10)

Coordinates of D = (-10,8)

Coordinates of G = (-1,-4)

Now, slope (m) between two points is given by :

`m=(y_2-y_1)/(x_2-x_1)`

`\text{Slope of AC, }m_1=(0-4)/(-4-(-7))\\\\\text{And, Slope of DG, }m_2=(-4-8)/(-1-(-10))\\\\\text{Now, putting }m_1=m_2\\\\ \implies (0-4)/(-4-(-7))=(-4-8)/(-1-(-10))`

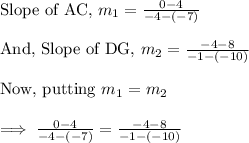
Hence, Option D is correct.