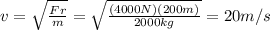Question

A 2000 kg car is rounding a curve of radius 200 m on a level road. The maximum frictional force the road can exert on the tires of the car is 4000 N. What is the highest speed at which the car can round the curve?

Answer 1

20 m/s

Step-by-step explanation:

The frictional force the road exerts on the car provides the centripetal force that keeps the car in circular motion along the curve:

`F=m(v^2)/(r)`

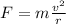
where

F is the centripetal force

m is the mass of the car

r is the radius of the curve

v is the speed of the car

In this problem we have:

m = 2000 kg

r = 200 m

F = 4000 N is the maximum force

Re-arranging the equation, we can calculate the maximum speed v corresponding to this force:

`v=\sqrt{(Fr)/(m)}=\sqrt{((4000 N)(200 m))/(2000 kg)}=20 m/s`