I'll denote the identity function by
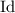 . Then for any functions
. Then for any functions
 with inverse
with inverse
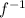 ,
,
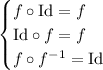
One important fact is that composition is associative, meaning for functions
 , we have
, we have
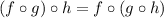
So given
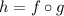
we can compose the functions on either side with
 :
:
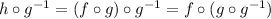
then apply the rules listed above:
