Question

The figure below shows three quadrilaterals on a coordinate grid.

Which of the following statements is true about the three quadrilaterals? Q and W are similar but not congruent.
W and S are similar and congruent.
W and Q are similar and congruent.
Q and S are similar but not congruent.

Answer 1

correct answers are option 1 (Q and W are similar but not congruent) and option 4 (Q and S are similar but not congruent)

Explanation:

Congruent:

Two quadrilateral are said to be congruent if they have equal length and breadth and they have exactly same shape.

Similar:

Two quadrilaterals will said to be similar if their sides are proportional . It means ratio of their length is equal to the ratio of their breath then the quadrilateral will said to be similar.

From the given graph it is clear that each angle of quadrilaterals Q, S and W is equal to
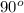`90^(o)` therefore these all quadrilaterals are rectangles.

In graph it is given that,

The length of rectangle is

`L_(1)= 5 units`

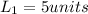
The length of rectangle Q is

`L_(2)= 5 units`

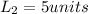
Breadth of rectangle S

`B_(1)= 2 units`

Breadth of rectangle Q

`B_(2)= 2 units`

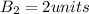
Therefore, it is clear that length and breadth of rectangle Q are equal to length and breadth of rectangle S and all the angles of Q and S are equal to
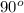`90^(o)` therefore, quadrilaterals Q and S are similar and congruent.

From graph it is given,

The length of rectangle W is

`L_(3)= 10 units`

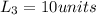
Breadth of rectangle S

`B_(3)= 4 units`

Therefore,

`(L_(1) )/(L_(3) ) =(5)/(10) =(1)/(2) \\(B_(1) )/(B_(3) )=(2)/(4) =(1)/(2)`

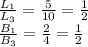
It means ratio of lengths of quadrilateral Q and W is equal to the ratio of their breaths. Therefore W and Q are said to be similar not congruent as they have different lengths and breadths.

Similarly,

ratio of lengths of quadrilateral S and W is equal to the ratio of their breaths. Therefore S and W are said to be similar not congruent as they have different length and breadth.

Answer 2

Answer: Q and W are similar but not congruent

Explanation:

From the given graph, The length of rectangle Q= 5 units

and the width of rectangle Q=2 units

The length of rectangle S= 5 units

and the width of rectangle S=2 units

Since the dimensions of rectangle Q is equals to the corresponding dimensions of the rectangle S and since all the angles of rectangle are right angles.

therefore, Q and S are similar and congruent as they have the same shape and the same size.

But The length of rectangle W= 10 units = 2 times length of Q

and the width of rectangle W=4 units= 2 times width of Q

Thus the dimensions of W is proportional to dimensions of Q.

Thus, Q and W are similar but not congruent.