Question

Identify square root of 11 as either rational or irrational, and approximate to the tenths place. Rational: square root of 11 ≈ 3.3 Rational: square root of 11 ≈ 3.4 Irrational: square root of 11 ≈ 3.3 Irrational: square root of 11 ≈ 3.4

Answer 1

Irrational: √11 ≈ 3.3

Explanation:

Rational numbers are numbers that can be expressed as a fraction. Irrational numbers are decimals that are non-terminating and non-repeating, such as 4.56789... Irrational numbers include π and non-perfect squares such as √7 because when calculated, these numbers are decimals that have no end and no pattern of repetition. Since there is not a number we can multiply by itself (such as 5 x 5 = 25) to get 11, then it is a non-perfect square and thus, irrational. When you calculate √11 you get a non-terminating decimal: 3.316624... When we round the nearest tenths place, the answer is approximately 3.3.

Answer 2

`√(11)\text{ is a irrational number}, √(11)\approx 3.3`

C is correct

Explanation:

Given:
`√(11)`

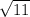
Rational number: A number in the form of division of two integers.
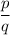`(p)/(q)` where
`q\\eq 0`

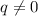
Irrational number: A number can not write as division of two integers.

Example:
`\pi,e,√(5)`

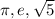
Therefore,
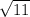`√(11)` is a irrational number.

Using calculator to find
`√(11)`

`√(11)=3.316....`

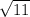
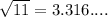
Now round off to tenths place.

`√(11)\approx 3.3`

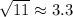
Hence,
`√(11)\text{ is a irrational number}, √(11)\approx 3.3`