Question

**URGENT** Roberto plans to use two transformers to reduce a voltage of 120 V to 4 V. He uses a transformer that has 300 coils in the primary winding and 50 coils in the secondary winding. He has four other transformers, as listed in the table. Which transformer should Roberto use to have an ending voltage of 4 V?

A- W

B-X

C- Y

D- Z

Answer 1

B) X

Step-by-step explanation:

Answer 2

As we know that in transformers we have

`(V_s)/(V_p) = (N_s)/(N_p)`

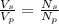
here we know that

`V_s = 4 Volts`

`V_p = 120 Volts`

`N_s = 50 coils`

`N_p = 300 coils`

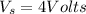
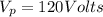
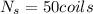
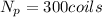
now from above equation we will have

`(V)/(120) = (50)/(300)`

`V = 20 Volts`

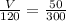
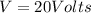
now we have to reduce this voltage to final voltage of V = 4 V

so again we will have

`(V_s)/(V_p) = (N_s)/(N_p)`

`(4)/(20) = (N_s)/(N_p)`

`(N_s)/(N_p) = (1)/(5)`

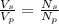
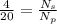
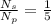
so we need to take such a winding whose ratio is 1:5

So it is satisfied in X

`N_p = 60`

`N_s = 12`

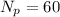
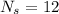
so answer will be

B)- X