Question

asked Jul 27, 2020 192k views

1 Answer

Tal Folkman · Answer 1 · 2020-08-02T23:09:53+0000

Answer:

a.
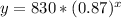
y=830*(0.87)^x

b. The value of stereo system after 2 years will be $628.23.

c. After approximately 4.98 years the stereo will be worth half the original value.

Explanation:

Let x be the number of years.

We have been given that you purchased a stereo system for $830. The value of the stereo system decreases 13% each year.

a. Since we know that an exponential function is in form:
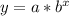y=a*b^x , where,

a = Initial value,

b = For decay b is in form (1-r), where r is rate in decimal form.

Let us convert our given rate in decimal form.

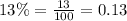
$13\%=(13)/(100)=0.13$

Upon substituting our given values in exponential decay function we will get

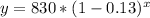
y=830*(1-0.13)^x

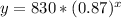
y=830*(0.87)^x

Therefore, the exponential model
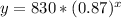represents the value of the stereo system in terms of the number of years since the purchase.

b. To find the value of stereo system after 2 years we will substitute x=2 in our model.

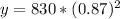
y=830*(0.87)^2

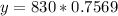
y=830*0.7569

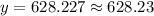
$y=628.227\approx 628.23$

Therefore, the value of stereo system after 2 years will be $628.23.

c. The half of the original price will be
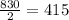(830)/(2)=415 .

Let us substitute y=415 in our model to find the time it will take the stereo to be worth half the original value.

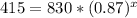
415=830*(0.87)^x

Upon dividing both sides of our equation by 830 we will get,

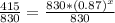
(415)/(830)=(830*(0.87)^x)/(830)

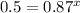
0.5=0.87^x

Let us take natural log of both sides of our equation.

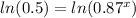
ln(0.5)=ln(0.87^x)

Using natural log property
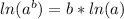ln(a^b)=b*ln(a) we will get,

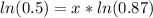
ln(0.5)=x*ln(0.87)

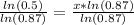
(ln(0.5))/(ln(0.87))=(x*ln(0.87))/(ln(0.87))

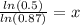
(ln(0.5))/(ln(0.87))=x

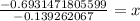
(-0.6931471805599)/(-0.139262067)=x

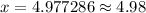
$x=4.977286\approx 4.98$

Therefore, after approximately 4.98 years the stereo will be worth half the original value.

Please log in or register to add a comment.