Question

Jen buys sesame bagels and plain bagels. If the ratio of sesame to plain is 1:3 and Jen bought 2 dozen bagels, what percent of bagels are plain? How many bagels are plain? Suppose each plain bagel has 0.53 gram of salt, and each sesame bagel has 0.65 gram. Use a percent to compare the amount of salt in a plain bagel to that in a sesame bagel.

Answer 1

The number of plain bagels are 18 and it is 75% of the total bagels .

The amount of salt in a plain bagel to that in a sesame bagel is 81.5% .

Explanation:

Formula

`Percentage = (Part\ value* 100)/(Total\ value)`

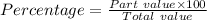
As given

Jen buys sesame bagels and plain bagels. If the ratio of sesame to plain is 1:3 and Jen bought 2 dozen bagels .

As one dozens contains 12 items .

Thus

Total number of bagels bought by Jen = 2 × 12

= 24

Let us assume that the x be the scalar multiple of sesame bagels and plain bagels .

Number of sesame bagels = 1x

Number of plain bagels = 3x

Than the equation becomes

x + 3x = 24

4x = 24

`x = (24)/(4)`

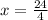
x = 6

Thus

Number of plain bagels = 3 × 6

= 18

Part value = 18

Total value = 24

Putting all the values in the formula

`Percentage = (18* 100)/(24)`

`Percentage = (1800)/(24)`

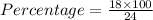
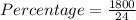
Percentage = 75 %

Therefore the number of plain bagels are 18 and it is 75% of the total bagels .

As given

Suppose each plain bagel has 0.53 gram of salt, and each sesame bagel has 0.65 gram.

Part value = 0.53 grams

Total value = 0.65 grams

Putting all the values in the formula

`Percentage = (0.53* 100)/(0.65)`

`Percentage = (5300)/(65)`

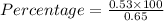
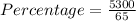
Percentage = 81.5 %

Therefore the amount of salt in a plain bagel to that in a sesame bagel is 81.5% .