Question

Which function is undefined for x = 0? y=3√x-2 y=√x-2 y=3√x+2 y=√x=2

Answer 1

B on EDGE

Explanation:

Answer 2

For this case, we have to:

By definition, we know:

The domain of
`f (x) = \sqrt [3] {x}` is given by all real numbers.

Adding or removing numbers to the variable within the root implies a translation of the function vertically or horizontally. In the same way, its domain will be given by the real numbers, independently of the sign of the term inside the root. Thus, it will always be defined.

So, we have:

`y = \sqrt [3] {x-2}` with
`x = 0`:
`y = \sqrt [3] {- 2}` is defined.

`y = \sqrt [3] {x+2}`with
`x = 0:\ y = \sqrt [3] {2}` is also defined.

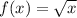`f (x) = \sqrt {x}`has a domain from 0 to ∞.

Adding or removing numbers to the variable within the root implies a translation of the function vertically or horizontally. For it to be defined, the term within the root must be positive.

Thus, we observe that:

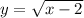`y = \sqrt {x-2}` is not defined, the term inside the root is negative when
`x = 0`.

While
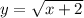`y = \sqrt {x+2}` if it is defined for
`x = 0`.

Answer:

`y = \sqrt {x-2}`

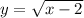
Option b