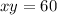Answer:
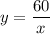 or
or
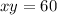 (depending on your teacher's format preference)
(depending on your teacher's format preference)
Explanation:
Proportionality background
Proportionality is sometimes called "variation". (ex. " 'y' varies inversely as 'x' ")
There are two main types of proportionality/variation:
- Direct
- Inverse.
Every proportionality, regardless of whether it is direct or inverse, will have a constant of proportionality (I'm going to call it "k").
Below are several different examples of both types of proportionality, and how they might be stated in words:
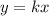 y is directly proportional to x
y is directly proportional to x
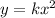 y is directly proportional to x squared
y is directly proportional to x squared
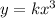 y is directly proportional to x cubed
y is directly proportional to x cubed
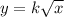 y is directly proportional to the square root of x
y is directly proportional to the square root of x
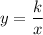 y is inversely proportional to x
y is inversely proportional to x
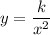 y is inversely proportional to x squared
y is inversely proportional to x squared
From these examples, we see that two things:
- things that are directly proportional -- the thing is multiplied to the constant of proportionality "k"
- things that are inversely proportional -- the thing is divided from the constant of proportionality "k".
Looking at our question
In our question, y is inversely proportional to x, so the equation we're looking at is the following
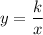 .
.
It isn't yet clear what the constant of proportionality "k" is for this situation, but we are given enough information to solve for it: "When y=12, x=5."
We can substitute this known relationship pair, and find the "k" that relates this pair of numbers:
Solving for k, and finding the general equation
General Inverse variation equation...
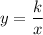
Substituting known values...
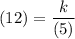
Multiplying both sides by 5...
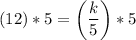
Simplifying/arithmetic...
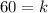
So, for our situation, k=60. So the inverse proportionality relationship equation for this situation is
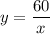 .
.
The way your question is phrased, they may prefer the form: