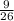Answer:
The correct option is B)
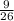
Explanation:
Consider the provided equations:
 and
and
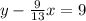
The above equation can be written as:
 and
and
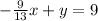
As it is given that we need to eliminate the variable x.
Multiplying the equation
 with
with
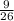 .
.
Therefore,
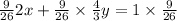
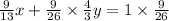
Therefore, the correct option is B)